
Although mathematics is incredibly tricky, there are numerous approaches to studying the subject that make it more accessible and enjoyable. From science and technology to finance and related fields, mathematics is essential for gaining insight into the world. Math is a universal language for conveying ideas across disciplines, and it is used to resolve issues and make forecasts.
Not only are mathematical equations functional, but many of them are also rather lovely. And many scientists acknowledge that they frequently enjoy some formulas for their function, aesthetics, and the straightforward, artistic truths they carry.
Have you ever considered using great equations and simple explanations to make math problems enjoyable to solve? If not, then this guide is your cue to start right now. These amusing and simple equations could be useful in daily life and might even surprise and amuse you along the road!
1. Pythagorean Theorem
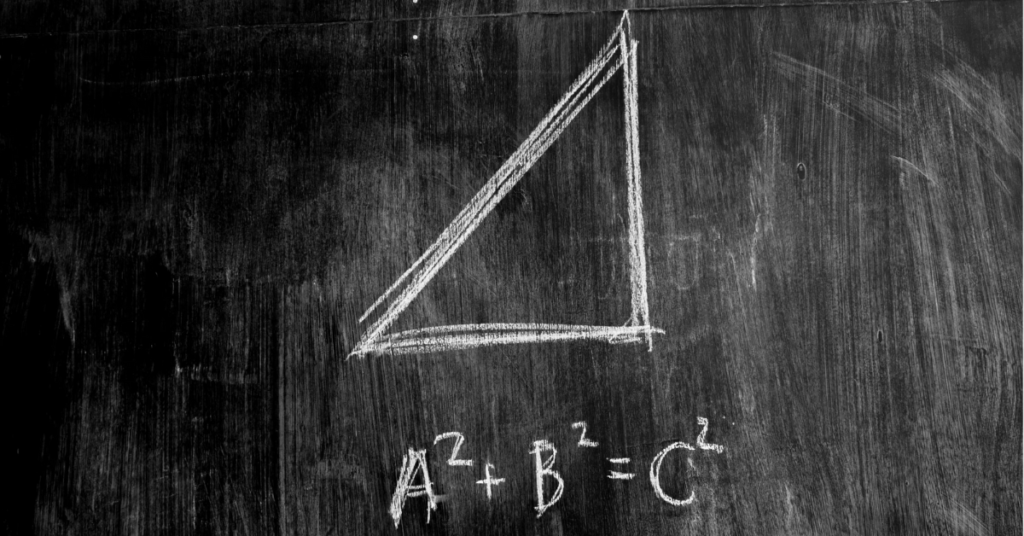
Understanding the Pythagorean Theorem is crucial for many fields of study, as it is a foundational mathematical concept. It is the initial concept taught to all children in geometry!
It implies that the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the other two sides. This theorem, referred to as Pythagoras after the classical Greek mathematician of the same name, has been known for many centuries.
Three interesting facts about the theorem that makes it fun include:
- It is thought that the Indians and ancient Babylonians utilized the Pythagorean Theorem. (facts for kids)
- The Pythagorean Theorem has several practical uses, such as navigation, engineering, and building.
- The theorem inspired mathematician Daina Taimina of Cornell University, and she has enjoyed it since childhood.
2. Euler’s Formula
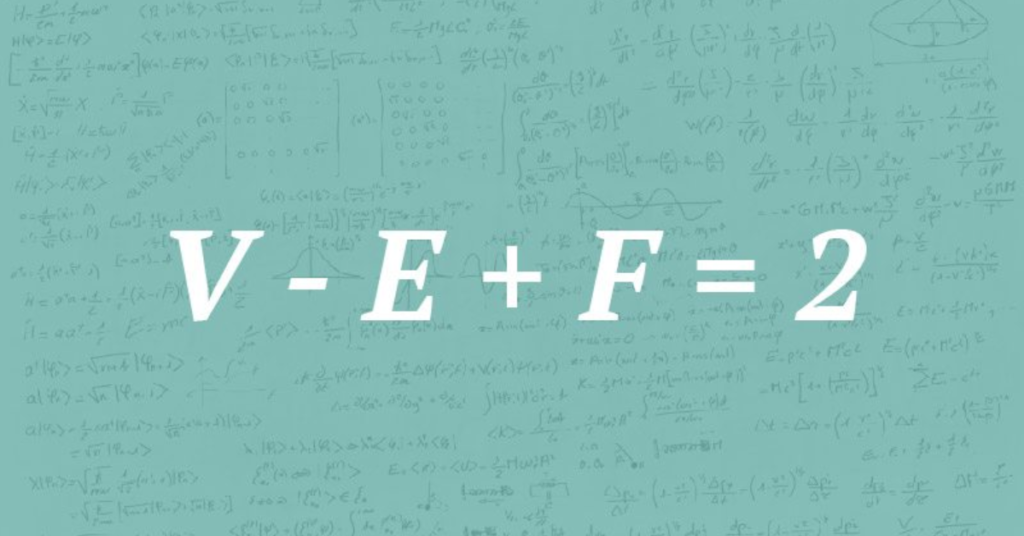
It is written as F + V = E + 2, where F is the number of faces, V is the number of vertices, and E is the number of edges.
Euler’s equation connects the five fundamental mathematical constants (e, I, pi, 0, and 1), making it widely regarded as one of the most beautiful equations in mathematics. The equation has numerous real-world uses in physics, engineering, and other disciplines. For instance, it is used in signal processing to examine the frequency content of signals.
Sometimes called “the most beautiful equation,” Euler’s identity is a mathematical equivalence likened to a Shakespearean sonnet. The late renowned physicist Richard Feynman referred to Euler’s Formula as “our gem” and “the most astonishing formula in mathematics” in his lectures. This is a specific instance of this formula.
3. The Theory Of Special Relativity
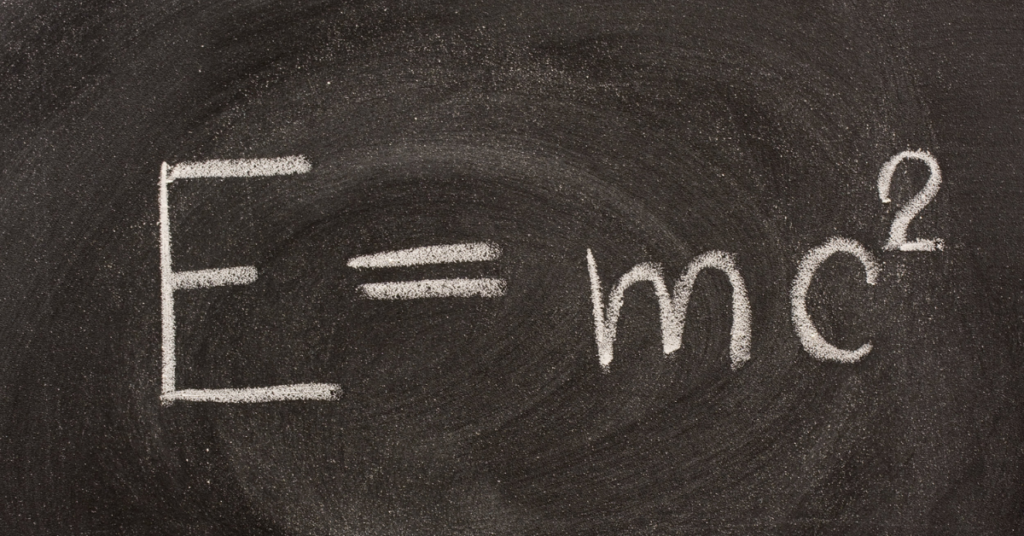
Developed by Albert Einstein, the Theory of Special Relativity describes the behavior of physical laws in the absence of gravity and introduces the notion that the speed of light is constant for all observers despite their relative velocity.
Time dilation, in which the passage of time is altered for things moving concerning one another, was also presented by this idea. The following formula summarizes the theory:
E = mc²
where c is the speed of light, m is mass, and E represents energy.
The fact that these rules hold for everyone, everywhere, and at all times, even deep within gravitational fields of all magnitudes, is what makes special relativity so “special.” Another fact that makes this equation fun and interesting is that the hypothesis significantly influences contemporary physics, resulting in the creation of cosmology, particle physics, and quantum mechanics!
4. Quadratic Equation
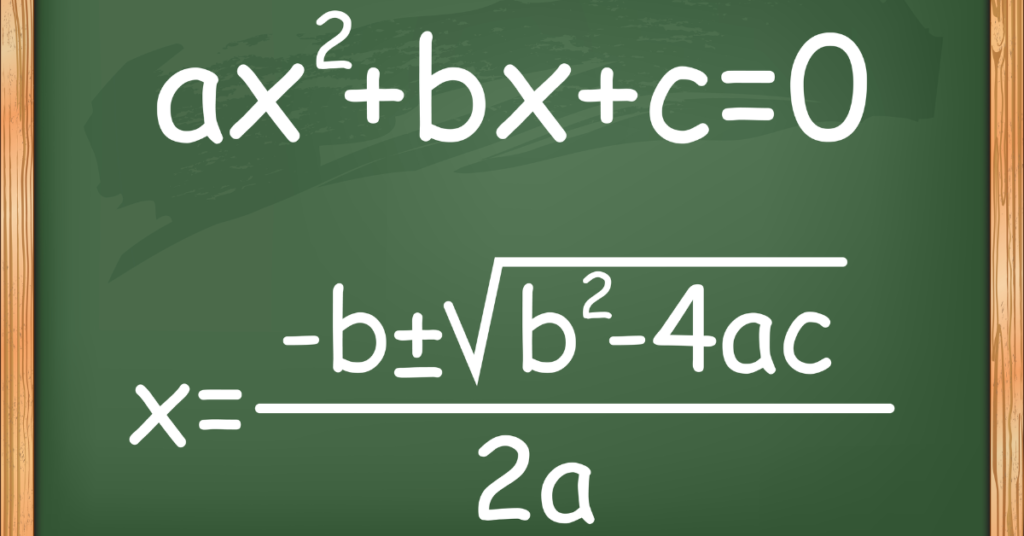
Mathematical expressions of the type ax2 + bx + c = 0 are known as quadratic equations. In these expressions, x is the unknown variable while a, b, and c are constants. The quadratic formula (-b sqrt(b2 – 4ac)) / 2a, which yields the values of x that make the equation true, may be used to solve this problem.
Applications of quadratic equations may be found in many branches of mathematics and science, such as physics, engineering, and finance! What, then, makes quadratic functions significant and fun?
Quadratic functions are unique in the academic curriculum. They are minor improvements over linear functions and provide a substantial break from attachment to straight lines since their values may be readily derived from input values.
5. Maxwell’s Equations
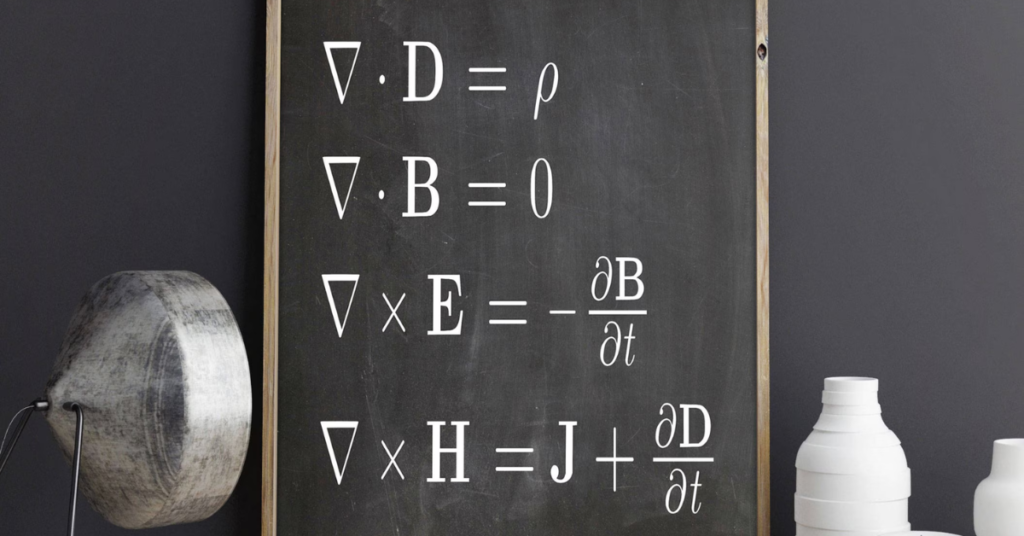
The four equations known as Maxwell’s explain the behavior of electromagnetic and electric fields and the interaction of charged particles and are considered the cornerstone of classical electromagnetism.
This group includes Gauss’s Law, Gauss’s Law for Magnetism, Faraday’s Law, and the Ampere-Maxwell Law, all of which were developed by James Clerk Maxwell in the nineteenth century. These equations have several practical applications, describing a wide range of electromagnetic events together.
Maxwell’s Equations explain numerous electromagnetic phenomena, combine electricity and magnetism, and have various technological and scientific applications ranging from wireless communication to electric motors and generators. They are crucial to our ability to make sense of contemporary technology!
6. Law Of Sines
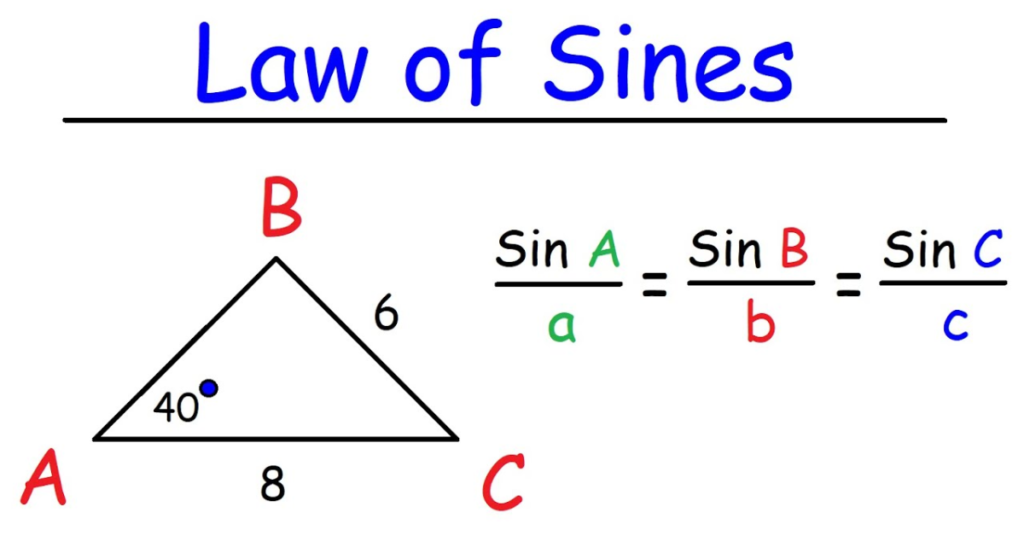
The trigonometric formula, the Law of Sines, establishes a relationship between the lengths of a triangle’s sides and the sine of the complementary angle. In particular, all three of a triangle’s sides have the same length ratio to the sine of the angle opposite that side.
When a, b, and c are the lengths of the sides of the triangle and A, B, and C are the opposing angles, this is written mathematically as a/sin(A) = b/sin(B) = c/sin(C). When only partial information about a triangle is given, this formula may be used to determine the missing side lengths or angles.
According to many students, it is a fun equation and has significance in real life, too; a sine bar is an engineering tool that measures tilt angle using the sine rule. Distance measurement in navigation and interstellar distance measurement are two more popular uses.
7. Fibonacci Sequence
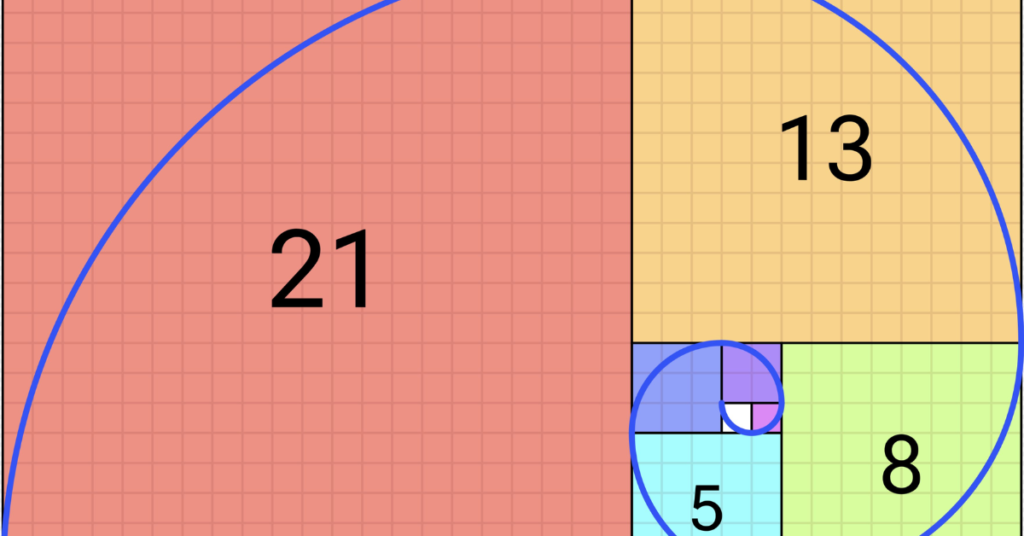
Starting with 0 and 1, the Fibonacci Sequence is a set of numbers where each one is the sum of the two numbers before it. Fn = Fn-1 + Fn-2 is the formula for the nth term in the Fibonacci Sequence, where F0 = 0 and F1 = 1.
Any term in the series may be generated using this recursive formula. The golden ratio, which has significant mathematical and aesthetic qualities, is close to being reached by the percentage of successive terms in the Fibonacci Sequence.
It is yet another fun equation and method adored by many, and apart from this, it holds significance in daily life matters as well! Some traders think that the Fibonacci ratios and numbers produced by the Sequence significantly impact finance and may be used by traders to their advantage when doing technical analysis.
8. Pi
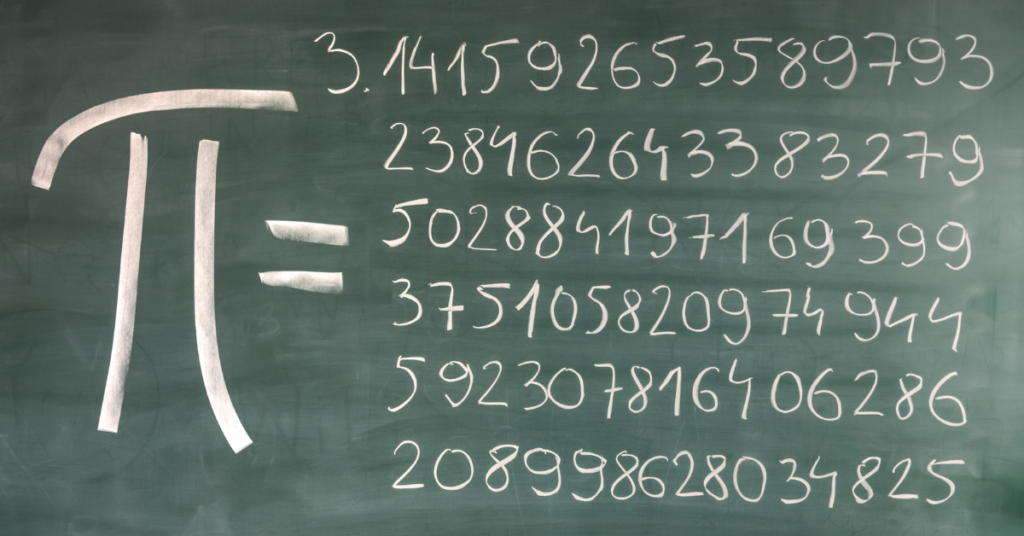
You may remember this equation from high school more than any other. It quantifies how large a circle’s radius is about its overall size. Its decimal value is written as 3.14159; yes, the value of Pi has almost 39 decimal places!
Here are three interesting facts that make Pi an amazing and interesting math equation:
- The number Pi has inspired a whole language! Each word in “Pi-lish” has the same number of letters as a digit of pi.
- The Dutch-German mathematician Ludolph van Ceulen devoted much of his life to calculating the first 36 digits of pi because of its allure. This fascination lasted as late as the 16th century.
- According to many mathematicians, it is more accurate to state that a circle has infinite corners rather than none. It is logical to suppose that the infinite number of pi digits and circle corners are related.
9. The Logistic Map

The Logistic Map is used to simulate population expansion over time. A population expands as a result of two factors: reproduction and competition for scarce resources, as shown by the recursive formula. Xn+1 = rXn(1 – Xn), where Xn is the population size at time n, r is a growth rate parameter, and (1 – Xn) measures resource availability.
The Logistic Map is a simple model that displays complicated behavior, such as chaos, bifurcations, and period doubling. It has uses in physics, economics, and several other disciplines, including biology.
The equation is exciting and fun for a variety of reasons. However, The logistic map is well-known for two reasons: first, it provides a method for forecasting how an animal population would change over time; second, it serves as an example of the exciting phenomena known as mathematical chaos.
10. Chaos Theory
Chaos theory studies systems that are very sensitive to their original circumstances, meaning that even slight changes to the beginning conditions may have enormous consequences down the line.
Applications may be found in physics, biology, economics, and engineering, and the study of how random or chaotic behavior can arise from deterministic systems is a central focus. Strange attractors, fractals, and bifurcation are all central ideas.
Several mathematicians and scientists contributed to creating chaos theory, which has since been applied to many other scientific disciplines!
Conclusion
All ages may benefit from studying mathematics by using pleasant and straightforward equations. These equations have practical applications and may be used to teach basic mathematical ideas in areas like algebra, geometry, and trigonometry. Learning math via enjoyable and straightforward equations helps enhance analytical, problem-solving, and critical thinking abilities while igniting curiosity and creativity!




