
For decades, mathematics has been a fascinating and challenging topic. People have been interested in learning and getting good at math from ancient Greeks to modern mathematicians. But have you ever wondered which math problem is the most challenging?
What could be so tricky and complicated that only some of the brightest mathematicians have been able to solve it? This article will look at 13 of the hardest math problems and how mathematicians have tried to solve them.
Continue reading the article to explore the world’s hardest math problems, listed below.
- The Poincaré Conjecture
- The Prime Number Theorem
- Fermat’s Last Theorem
- The Reimann Hypothesis
- Classification of Finite Simple Groups
- Four Color Theorem
- Goldbach’s Conjecture
- Inscribed Square Problem
- Twin Prime Conjecture
- The Continuum Hypothesis
- Collatz Conjecture
- Birch and Swinnerton-Dyer conjecture
- The Kissing Number Problem
The Poincaré Conjecture
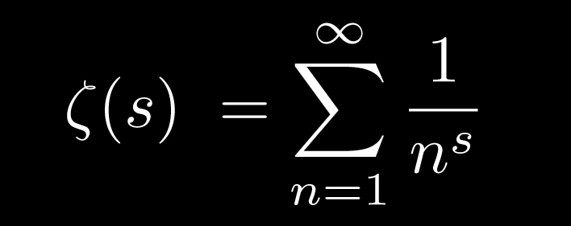
Mathematicians struggled for about a century with the Poincaré conjecture, which was put forth by Henri Poincaré in 1904.
According to this theory,
every closed, connected three-dimensional space is topologically identical to a three-dimensional sphere (S3).
We must explore the field of topology to comprehend what this entails. The study of properties of objects that hold after being stretched, bent, or otherwise distorted is known as topology. In other words, topologists are fascinated by how things can change without rupturing or being torn.
The topology of three-dimensional spaces is the subject of the Poincaré conjecture. A space volume with three dimensions—length, breadth, and height—is a three-dimensional space. A three-dimensional object called a sphere has a round and curved surface.
According to the Poincaré Conjecture, a three-sphere (S3), or the collection of points in four dimensions that are all at a fixed distance from a given point, is topologically identical to every simply-connected, closed, three-dimensional space (i.e., one that has no gaps or voids) and edges.
Solution
Although it would appear easy, it took more than a century to confirm the conjecture thoroughly.
- Poincaré expanded his hypothesis to include any dimension (n-sphere).
- Stephen Smale, an American mathematician, proved the conjecture to be true for n = 5 in 1961.
- Freedman, another American mathematician, proved the conjecture to be true for n = 4 in 1983.
- Grigori Perelman, a Russian mathematician, then proved the conjecture to be true for n = 3 in 2002, completing the solution.
- Perelman eventually addressed the problem by combining topology and geometry. One of the highest awards in mathematics, the Fields Medal, was given to all three mathematicians. Perelman rejected the Fields Medal. He was also given a $1 million prize by the Clay Mathematics Institute (CMI) of Cambridge, Massachusetts, for resolving one of the seven Millennium Problems, considered one of the world’s most challenging mathematical puzzles. However, he turned it down as well.
The Prime Number Theorem
The prime number theorem (PNT) explains how prime numbers asymptotically distribute among positive integers. It shows how fast primes become less common as numbers get bigger.
The prime number theorem states that the number of primes below a given natural number N is roughly N/log(N), with the word “approximately” carrying the typical statistical connotations.
Solution
- Two mathematicians, Jacques Hadamard and Charles Jean de la Vallée Poussin, independently proved the Prime Number Theorem in 1896. Since then, the proof has frequently been the subject of rewrites, receiving numerous updates and simplifications. However, the theorem’s influence has only increased.
Fermat’s Last Theorem
French lawyer and mathematician Pierre de Fermat lived in the 17th century. Fermat was one of the best mathematicians in history. He talked about many of his theorems in everyday conversation because math was more of a hobby for him.
He made claims without proof, leaving it to other mathematicians decades or even centuries later to prove them. The hardest of them is now referred to as Fermat’s Last Theorem.
Fermat’s last theorem states that;
there are no positive integers a, b, and c that satisfy the equation an + bn = cn for any integer value of n greater than 2.
Solution
- In 1993, British mathematician Sir Andrew Wiles solved one of history’s longest mysteries. As a result of his efforts, Wiles was knighted by Queen Elizabeth II and given a special honorary plaque rather than the Fields Medal because he was old enough to qualify.
- Wiles synthesized recent findings from many distinct mathematics disciplines to find answers to Fermat’s well-known number theory query.
- Many people think Fermat never had proof of his Last Theorem because Elliptic Curves were utterly unknown in Fermat’s time.
The Reimann Hypothesis
Mathematicians have been baffled by the Riemann Hypothesis for more than 150 years. It was put forth by the German mathematician Bernhard Riemann in 1859. According to Riemann’s Hypothesis
Every Riemann zeta function nontrivial zero has a real component of ½.
The distribution of prime numbers can be described using the Riemann zeta function. Prime numbers, such as 2, 3, 5, 7, and 11, can only be divided by themselves and by one. Mathematicians have long been fascinated by the distribution of prime numbers because figuring out their patterns and relationships can provide fresh perspectives on number theory and other subject areas.
Riemann’s hypothesis says there is a link between how prime numbers are spread out and how the zeros of the Riemann zeta function are set up. If this relationship is accurate, it could significantly impact number theory and help us understand other parts of mathematics in new ways.
Solution
- The Riemann Hypothesis is still unproven, despite being one of mathematics’ most significant unsolved issues.
- Michael Atiyah, a mathematician, proclaimed in 2002 that he had proved the Riemann Hypothesis, although the mathematical community still needs to acknowledge his claim formally.
- The Clay Institute has assigned the hypothesis as one of the seven Millennium Prize Problems. A $1 million prize is up for anyone who can prove the Riemann hypothesis to be true or false.
Classification of Finite Simple Groups
Abstract algebra can be used to do many different things, like solve the Rubik’s cube or show a body-swapping fact in Futurama. Algebraic groups follow a few basic rules, like having an “identity element” that adds up to 0.
Groups can be infinite or finite, and depending on your choice of n, it can be challenging to describe what a group of a particular size n looks like.
There is one possible way that the group can look at whether n is 2 or 3. There are two possibilities when n equals 4. Mathematicians intuitively wanted a complete list of all feasible groups for each given size.
Solution
- The categorization of finite simple groups, arguably the most significant mathematical undertaking of the 20th century, was planned by Harvard mathematician Daniel Gorenstein, who presented the incredibly intricate scheme in 1972.
- By 1985, the project was almost finished, but it had consumed so many pages and publications that peer review by a single person was impossible. The proof’s numerous components were eventually reviewed one by one, and the classification’s completeness was verified.
- The proof was acknowledged mainly by the 1990s. Verification was later streamlined to make it more manageable, and that project is still active today.
Four Color Theorem

According to four color theorem
Any map in a plane can be given a four-color coloring utilizing the rule that no two regions sharing a border (aside from a single point) should have the same color.
Solution
- Two mathematicians at the University of Illinois at Urbana-Champaign, Kenneth Appel and Wolfgang Hakan identified a vast, finite number of examples to simplify the proof. They thoroughly examined the over 2,000 cases with the aid of computers, arriving at an unheard-of proof style.
- The proof by Appel and Hakan was initially debatable because a computer generated it, but most mathematicians ultimately accepted it. Since then, there has been a noticeable increase in the usage of computer-verified components in proofs, as Appel and Hakan set the standard.
Goldbach’s Conjecture
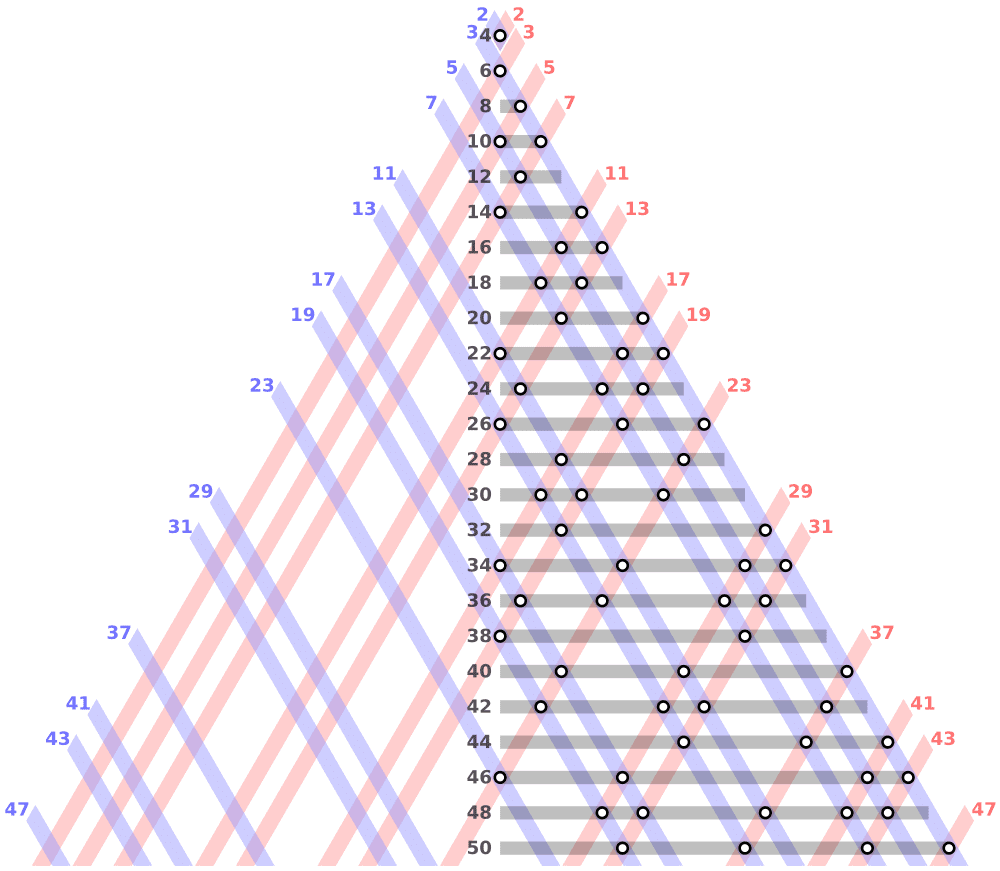
According to Goldbach’s conjecture, every even number (higher than two) is the sum of two primes. You mentally double-check the following for small numbers: 18 is 13 + 5, and 42 is 23 + 19. Computers have tested the conjecture for numbers up to a certain magnitude. But for all natural numbers, we need proof.
Goldbach’s conjecture resulted from correspondence between Swiss mathematician Leonhard Euler and German mathematician Christian Goldbach in 1742.
Solution
- Euler is regarded as one of the finest mathematicians in history. Although I cannot prove it, in the words of Euler, “I regard [it] as a totally certain theorem.”
- Euler might have understood why it is conversely tricky to resolve this problem. More significant numbers have more methods than smaller ones to be expressed as sums of primes. In the same way that only 3+5 can split eight into two prime numbers, 42 can be divided into 5+37, 11+31, 13+29, and 19+23. Therefore, for vast numbers, Goldbach’s Conjecture is an understatement.
- The Goldbach conjecture has been confirmed for all integers up to 4*1018, but an analytical proof has yet to be found.
- Many talented mathematicians have attempted to prove it but have yet to succeed.
Inscribed Square Problem
Another complex geometric puzzle is the “square peg problem,” also known as the “inscribed square problem” or the “Toeplitz conjecture.”
The Inscribe Square Problem Hypothesis asks:
Does every simple closed curve have an inscribed square?
In other words, it states, ” For any curve, you could draw on a flat page whose ends meet (closed), but lines never cross (simple); we can fit a square whose four corners touch the curve somewhere.
Solution
- The inscribed square problem is unsolved in geometry.
- It bears the names of mathematicians Bryan John Birch and Peter Swinnerton-Dyer, who established the conjecture using automated calculation in the first half of the 1960s.
- Only specific instances of the hypothesis have been proven as of 2023.
Twin Prime Conjecture
The Twin Prime Conjecture is one of many prime number-related number theory puzzles. Twin primes are two primes that differ from each other by two. The twin prime examples include 11 and 13 and 599 and 601. Given that there are an unlimited number of prime numbers, according to number theory, there should also be an endless number of twin primes.
The Twin Prime Conjecture asserts that there are limitless numbers of twin primes.
Solution
- In 2013, Yitang Zhang did groundbreaking work to solve the twin prime conjecture.
- However, the twin prime conjecture still needs to be solved.
The Continuum Hypothesis
Infinities are everywhere across modern mathematics. There are infinite positive whole numbers (1, 2, 3, 4, etc.) and infinite lines, triangles, spheres, cubes, polygons, etc. It has also been proven by modern mathematics that there are many sizes of infinity.
If the elements of a set can be arranged in a 1-to-1 correspondence with the positive whole numbers, we say the set of elements is countably infinite. Therefore, the set of whole numbers and rational numbers are countable infinities.
Georg Cantor found that the set of real numbers is uncountable. In other words, even if we used all the whole numbers, we would never be able to go through and provide a positive whole number to every real number. Uncountable infinities might be seen as “larger” than countable infinities.
Solution
- According to the continuum hypothesis, there must be a set of numbers whose magnitude strictly falls between countably infinite and uncountably infinite. The continuum hypothesis differs from the other problems in this list in that it is impossible to solve or at least impossible to address using present mathematical methods.
- As a result, even though we have yet to determine whether the continuum hypothesis is accurate, we do know that it cannot be supported by the tools of modern set theory either. It would be necessary to develop a new framework for set theory, which has yet to be done, to resolve the continuum hypothesis.
Collatz Conjecture
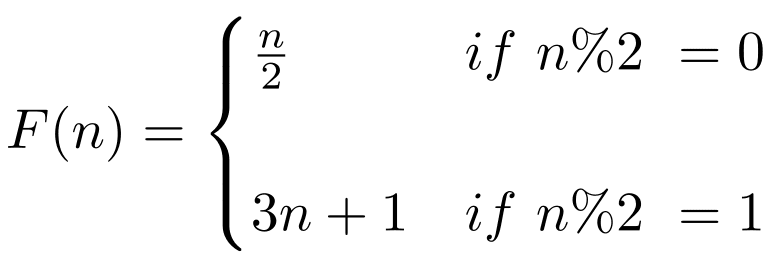
To understand Collatz’s conjecture, try to understand the following example.
First, you have to pick a positive number, n. Then, from the last number, create the following sequence:
If the number is even, divide by 2. If it’s odd, multiply by 3 and then add 1. The objective is to keep going through this sequence until you reach 1. Let’s try this sequence with the number 12 as an example. Starting with number 12, we get:
12, 6, 3, 10, 5, 16, 8, 4, 2, 1
Starting at 19, we obtain the following:
19, 58, 29, 88, 44, 22, 11, 34, 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1
According to the Collatz conjecture, this sequence will always end in 1, regardless of the value of n you started with. This speculation has been tested for all values of n up to 87,260, but no proof has been found.
Solution
- Collatz’s conjecture has been unsolved up till now.
- Mathematical problem-solver Paul Erdree once said of the Collatz Conjecture, “Mathematics may not be ready for such problems.”
Birch and Swinnerton-Dyer conjecture
Two British mathematicians, Bryan Birch and Peter Swinnerton-Dyer formulated their hypotheses in the 1960s. The Birch and Swinnerton-Dyer conjecture in mathematics describes rational answers to the equations defining an elliptic curve.
This hypothesis states explicitly that there are an infinite number of rational points (solutions) if ζ(1) equals 0 and that there are only a finite number of such places if ζ(1) is not equal to 0.
Solution
- For Birch and Swinnerton-Dyer’s conjecture, Euclid provided a comprehensive solution, but this becomes very challenging for problems with more complex solutions.
- Yu. V. Matiyasevich demonstrated in 1970 that Hilbert’s tenth problem could not be solved, saying there is no mechanism for identifying when such equations have a whole number solution.
- As of 2023, only a few cases have been solved.
The Kissing Number Problem

Each sphere has a Kissing Number, the number of other spheres it is kissing, when a group of spheres is packed together in one area. For example, your kissing number is six if you touch six nearby spheres. Nothing difficult.
Mathematically, the condition can be described by the average kissing number of a tightly packed group of spheres. However, a fundamental query regarding the kissing number remains unsolved.
First, you must learn about dimensions to understand the kissing number problem. In mathematics, dimensions have a special meaning as independent coordinate axes. The two dimensions of a coordinate plane are represented by the x- and y-axes.
A line is a two-dimensional object, whereas a plane is a three-dimensional object. Mathematicians have established the highest possible kissing number for spheres with those few dimensions for these low numbers. On a 1-D line, there are two spheres—one to your left and the other to your right.
Solution
- The Kissing Problem is generally unsolved in dimensions beyond three.
- A complete solution for the kissing problem number faces many obstacles, including computational constraints. The debate continued to solve this problem.
The Bottom Line
When it comes to pushing the boundaries of the enormous human ability to comprehend and problem-solving skills, the world’s hardest math problems are unquestionably the best. These issues, which range from the evasive Continuum Hypothesis to the perplexing Riemann Hypothesis, continue to puzzle even the sharpest mathematicians.
But regardless of how challenging they are, these problems keep mathematicians inspired and driven to explore new frontiers. Whether or not these problems ever get resolved, they illustrate the enormous ability of the human intellect.
Even though some of these issues might never fully be resolved, they continue to motivate and inspire advancement within the field of mathematics and reflects how broad and enigmatic this subject is!
Let us know out of these 13 problems which problem you find the hardest!





I want to be prodigy genius?