This article delves into the intriguing behavior of a bouncing ball, exploring its connection to the well-known “golf ball paradox.” We’ll embark on a journey that starts with a simple observation and unfolds to reveal the fascinating interplay between spin and trajectory.
The Curious Case of the Bouncing Ball
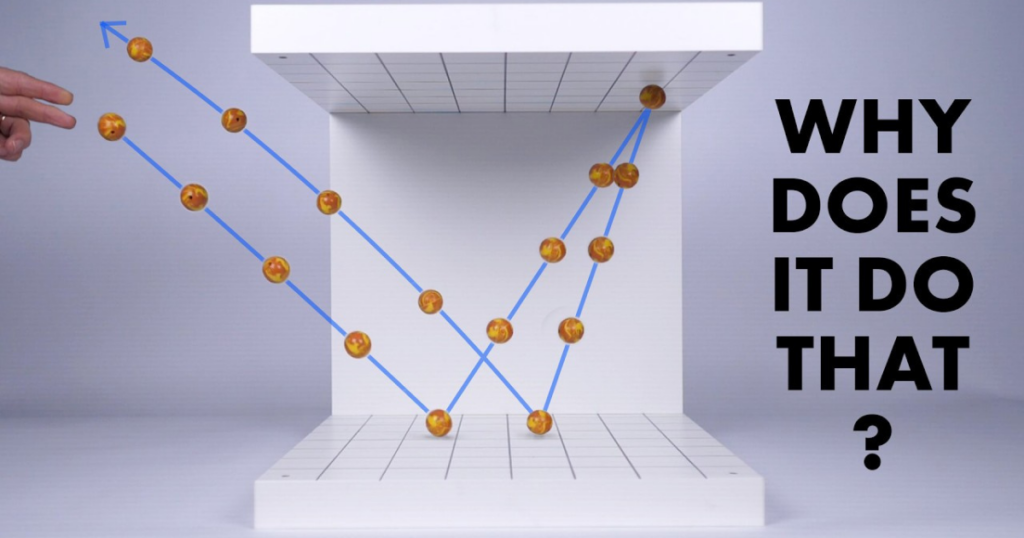
The article begins by highlighting the oddity of a ball bouncing under a table and consistently returning to the sender. It then establishes a link to the previously discussed golf ball paradox, where a spinning ball appears to defy logic by not simply oscillating up and down inside a cylinder.
Bridging the Gap: Discretizing the Problem
The key idea lies in “discretizing” the problem – breaking it down into smaller, more manageable steps. This approach involves imagining numerous tiny collisions happening in quick succession, mimicking the continuous rolling motion in the cylinder.
Understanding the Spin: A Ball’s Perspective
The article dives into the concept of spin and its crucial role in the ball’s behavior. It explains how the ball acquires spin upon hitting the ground and how this spin influences its subsequent bounces.
From Square to Cylinder: Increasing the Complexity

We then embark on a step-by-step exploration, starting with a ball bouncing between just two surfaces, like under a table. This is then extended to a square container, where the ball undergoes multiple bounces with each wall. The concept of spin axis is introduced, along with the crucial role of friction in modifying the ball’s trajectory.
Approaching the Cylinder: The Beauty of Limits

As the number of faces in the container increases (from square to octagonal and beyond), the scenario gradually approaches a smooth cylinder, essentially replicating the golf ball paradox setup. We see how the smaller, more frequent collisions contribute to the same overall effect observed in the cylinder.
Beyond the Paradox: Unveiling the Mechanism
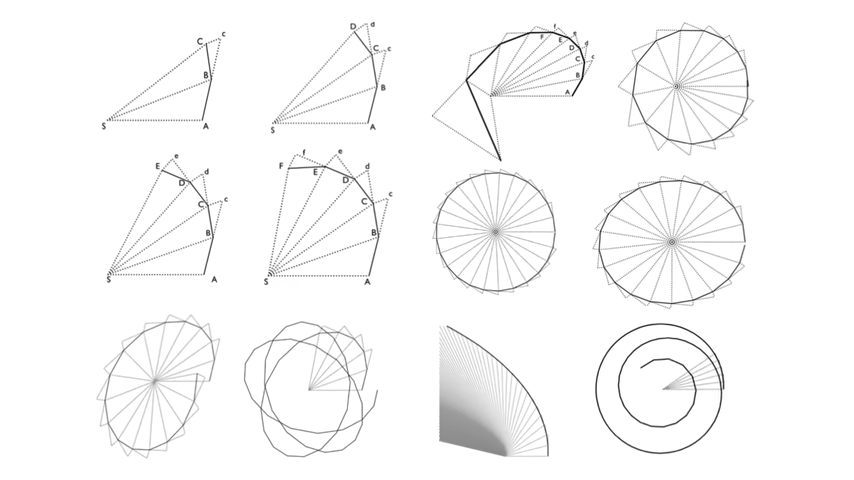
The article clarifies the misconception from the previous video about the ball’s spin axis being fixed like a gyroscope. It emphasizes that each bounce not only changes the ball’s direction but also modifies its spin. As the number of collisions tends to infinity in the cylinder case, these discrete changes in spin become a continuous process, explaining the observed behavior.
Expanding the Horizons: Simulations and Connections
The final section delves into the validation of the concept through simulations and explores the broader application of this “discretization” approach. It highlights the historical use of this method in understanding planetary orbits and its relevance in simulating the motion of charged particles.
In essence, this article provides a deeper understanding of the golf ball paradox by breaking it down into a series of intuitive steps, revealing the hidden interplay between spin and trajectory that governs the seemingly counterintuitive behavior of the bouncing ball.




