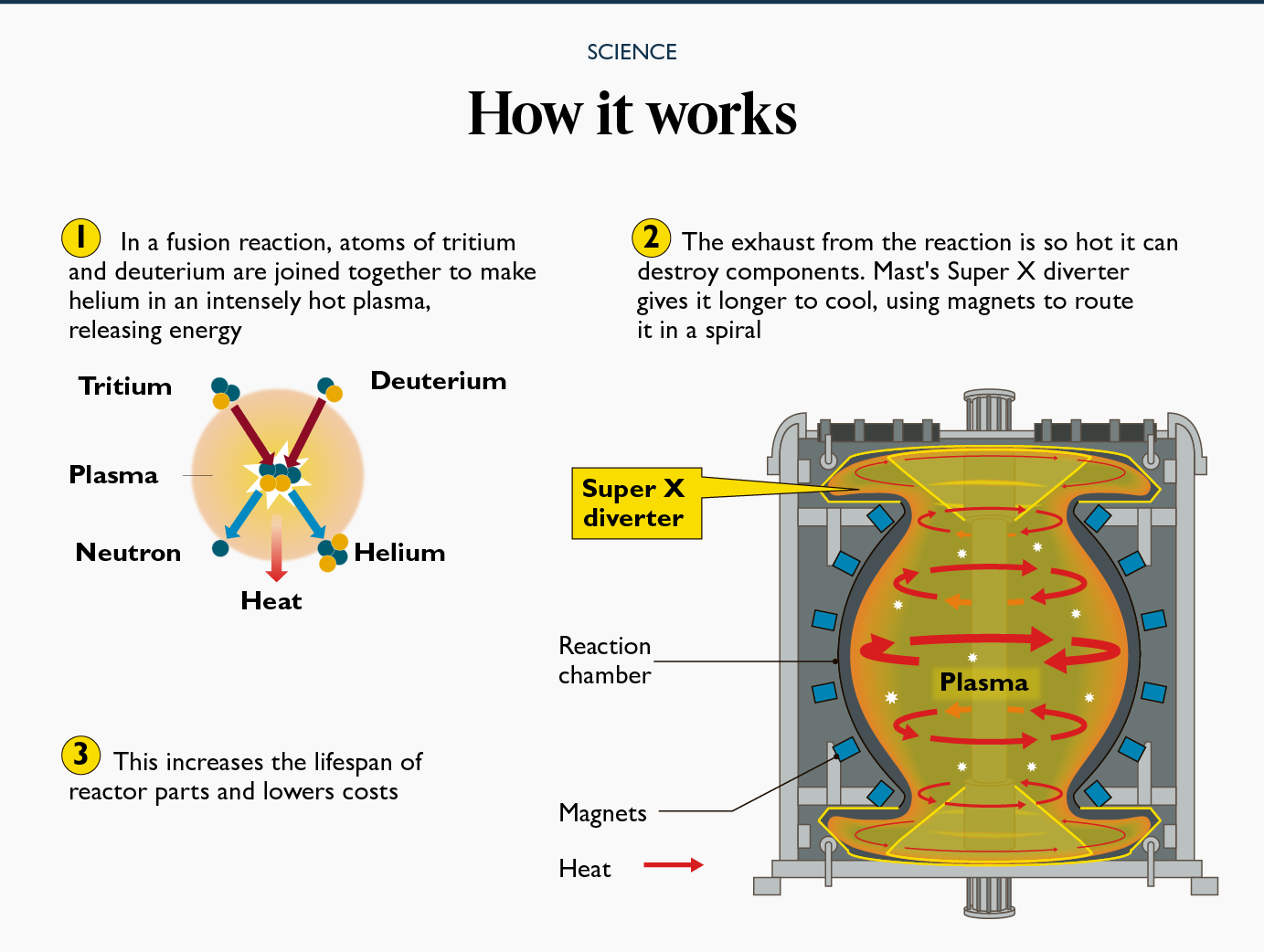
Mathematics is not a creation but rather a finding initially introduced to the world by Greek mathematicians. This is why the term mathematics is derived from the Greek word “mathema,” which means “knowledge.” Mathematics is a field of study concerned with the logical relationship between reason, amount, order, and shape. It was not found by a single mathematician but rather by a group of mathematicians worldwide working simultaneously. When did it first begin, though? The different kinds of maths we study today, like Algebra, Geometry, and Calculus, are not the beginning. Let’s talk about the people who made mathematical discoveries and the periods in which they occurred.
History of Mathematics
Ancient people were the first to adopt mathematics to count! Numerous times a day, we count using mathematics. Similarly, in ancient times, people used mathematics unconsciously to count, add, subtract, and divide, despite their lack of mathematical education.
Babylonian
Babylonian mathematics refers to any mathematics practiced by the peoples of Mesopotamia (now Iraq) from the time of the Sumerians to the Christian era. Sumerians, who built the first civilization in Mesopotamia, left the earliest evidence of mathematics in writing. In 3000 BCE, they created a sophisticated system of metrology. In 2500 B.C., the Sumerians used clay tablets to record multiplication tables, geometry exercises, and division problems. Additionally, the oldest evidence of Babylonian numbers dates to this time period.

In Babylonian mathematics, the sexagesimal (base-60) numeric system was used. This is the origin of the modern usage of 60 seconds per minute, 60 minutes per hour, and 360 degrees in a circle, and seconds and minutes of arc to represent fractions of a degree. In addition, the Babylonians used a place-value system in which, similar to the decimal system, numerals written in the left column represented greater values.
The strength of the Babylonian notational system resided in its ability to represent fractions as easily as whole numbers; consequently, the multiplication of two fractional values was identical to the multiplication of integers, similar to current notation. In addition to fractions, algebra, quadratic and cubic equations, and the calculation of regular numbers and their reciprocal pairs, other topics covered by Babylonian mathematics include algebra, calculus, and quadratic and cubic equations.
Egyptian
Egyptian mathematics is mathematics that is written in the Egyptian language. The most extensive Egyptian mathematical work is the Rhind papyrus (often sometimes referred to as the Ahmes papyrus after its author), which is dated to approximately 1650 B.C. but is presumably a copy of an older document from the Middle Kingdom between 2000 and 1800 B.C. It is a guidebook for students of mathematics and geometry. In addition to providing area formulas and methods for multiplication, division, and working with unit fractions, it provides evidence of other mathematical knowledge, such as composite and prime numbers, arithmetic, and geometric. It also demonstrates how to solve linear equations of the first order and arithmetic and geometric series.

The Moscow papyrus, likewise from the Middle Kingdom period and dating to perhaps 1890 B.C., is a notable Egyptian mathematical text. It comprises what is often known now as word problems. In addition, the ancient Egyptians were likely the first to employ measurement units. The Berlin Papyrus 6619 (about 1800 B.C.) demonstrates that ancient Egyptians could solve an equation of the second order.
Greek
Greek mathematics was significantly more advanced than the mathematics created by primary cultures. All surviving records of pre-Greek mathematics demonstrate the use of inductive reasoning or the utilization of repeated observations to build rules of thumb. In contrast, Greek mathematicians utilized deductive reasoning. The Greeks applied logic to deduce conclusions from definitions and axioms and mathematical rigor to demonstrate their validity. Although the extent of the effect is debatable, Egyptian and Babylonian mathematics likely inspired them.

The Pythagorean School was founded by Pythagoras, whose theory was mathematics dominated the universe”. Pythagoreans originated the term “mathematics,” and the study of mathematics begins with them. The Pythagoreans are credited with the first demonstration of the Pythagorean theorem and the evidence of the existence of irrational numbers. Still, the statement of the theorem has a lengthy history.
Archimedes of Syracuse (about 287–212 BC), usually regarded as the greatest mathematician of antiquity and the father of mathematics, utilized the method of exhaustion to compute the area under the arc of a parabola by summing an infinite series in a manner not different to modern calculus. He also demonstrated that the method of exhaustion could be used to compute the value with the appropriate degree of precision, and he produced the most precise value at the time. In addition, he investigated the spiral that bears his name and derived formulas for the volumes of surfaces of paraboloid, ellipsoid, and hyperboloid. His greatest accomplishment was determining the surface area and volume of a sphere by demonstrating that they are 2/3 the surface area and volume of a cylinder encircling the sphere.
Roman
Greek mathematics resumed during the Roman Republic and later during the Empire. The development of the Roman calendar also required elementary mathematics. During the Roman Empire in the eighth century B.C., the first calendar supposedly had 356 days plus a leap year every other year. Romans were competent at initiating and detecting financial fraud, as well as managing taxes for the treasury, through the use of arithmetic.

Siculus Flaccus, a Roman land surveyor, authored the Categories of Fields, which assisted Roman land surveyors in calculating the surface areas of allocated lands and territories. In addition to handling trade and taxes, the Romans routinely applied mathematics to engineering challenges, such as the construction of bridges, roads, and military campaigns.
Chinese
The oldest surviving Chinese mathematical literature would probably be the Tsinghua Bamboo Slips, which include the first known decimal multiplication table (the Babylonians had tables with a base of 60), dated to approximately 305 BC. Notable in Chinese mathematics is the adoption of a decimal positional writing system, the “rod numerals,” in which distinct ciphers were employed for integers between 1 and 10, as well as extra ciphers for powers of ten.

This was the world’s most advanced number system at the time. Rod numerals permitted the display of numbers of any size, and calculations could be performed on the Chinese abacus. The Chinese may have also been the first to calculate negative numbers and Pascal’s Triangle centuries before Pascal himself performed these calculations.
Indian
The oldest surviving mathematical documents from India are appendices to religious scriptures, dating between the eighth century B.C. and the second century A.D., that provide simple instructions for building altars of various forms, including squares, rectangles, parallelograms, and others. Additionally, they compute the square root of 2 to many decimal places, provide a list of Pythagorean triples, and express the Pythagorean theorem.

The subsequent important mathematical works from India are astronomical treatizes from the fourth and fifth centuries A.D. In contrast to Ptolemaic trigonometry, they contain the earliest instance of trigonometric relations based on the half-chord, as is the case in modern trigonometry. The English “sine” and “cosine” originate from the Sanskrit “jiya” and “kojiya” through a series of translation blunders.
Islamic
The Islamic world has been credited for preserving mathematical knowledge. In the eighth century, the Islamic Empire created in Persia, the Middle East, Central Asia, North Africa, Iberia, and portions of India made substantial contributions to mathematics. Although the majority of Islamic mathematical writings were written in Arabic, they were not written by Arabs. In the ninth century, the Persian mathematician Muhammad ibn Ms al-Khwarizmi published important works on Hindu–Arabic numerals and equation-solving techniques. The term algorithm is taken from the Latinization of Algoritmi’s name. He provided a comprehensive explanation for the algebraic solution of quadratic equations with positive roots, and he was the first to teach algebra in its most basic form.

He also described the essential methods of “reduction” and “balancing,” which refer to the inversion of subtracted terms to the opposite side of an equation, i.e., the elimination of like terms on opposite sides of the equation. In his book al-Fakhri, Al-Karaji made additional advances in algebra by extending the methodology to include integer powers and integer roots of unknown values. In the late 11th century, Omar Khayyam composed Discussions on the Difficulties in Euclid, a treatise detailing what he perceived to be errors in Euclid’s Elements, particularly the parallel postulate. In addition, he was the first person to discover the general geometric solution to cubic equations. He also had a significant impact on calendar change.
Famous Mathematicians and Their Discoveries

Archimedes – The Father of Mathematics
In 287 BC, Archimedes was born in Syracuse, Sicily. He was an ancient Greek mathematician. He is commonly referred to as the Father of Mathematics and is credited with developing modern mathematics. He created new methods for solving equations and comprehending geometric concepts.
Discovering how to compute the area of a circle was one of his most notable achievements. In addition, he invented a method for determining the volume of a spherical. These discoveries were crucial for comprehending the universe around us. In addition, he studied the spiral bearing his name and established formulas for the surface volumes of the paraboloid, ellipsoid, and hyperboloid.
Brahmagupta
Work by Brahmagupta consisted of principles for computing with zero. Historically, it served as a placeholder. In addition to mathematics, he produced significant achievements in astronomy. The Indian mathematician of the seventh century demonstrated how to find the cube and cube root of an integer and provided rules for squares and square roots.
Euler
Leonhard Euler was one of the mathematical titans of the 18th century. He was born in Basel, Switzerland. Euler invented, popularised, or standardized most of the notation used by mathematicians today, including e, I f(x) ∑, and the usage of a, b, and c as constants and x, y, and z as unknowns. His attempts to standardize these and other symbols (such as the trigonometric functions) contributed to the internationalization of mathematics and promoted problem-solving collaboration.
Diophantus
Due to the simplicity and originality of his algebraic equations, he was commonly hailed as the ‘Father of Algebra.’ He authored several books on algebra. Later, he became well-known for his book Arithmetica, which provided a brief explanation with examples of the optimal solution for all algebraic equations and the theory associated with numbers.
Thales
Thales of Miletus was one of the most renowned Greek mathematicians. He is also the first person credited with a mathematical discovery. He was an expert in Geometry and utilized it to calculate the heights of pyramids and determine the distance between a ship and the land. As he was also a philosopher, in the ‘Theorem of Thales,’ he attempts to apply Geometry through deductive reasoning and draws four corollaries as a result.
Pythagoras
Pythagoras of Samos was born in approximately 570 B.C. Many mathematical discoveries are attributed to Pythagoras, while his authenticity remains questionable. Perhaps the most well-known is the Pythagorean theorem (named after him). He may have also contributed to the development of the Theory of Proportions.
Euclid
Euclid was a well-known mathematician regarded as the ‘Father of Geometry.’ His famous contribution to geometry is referred to as Euclidean geometry, which appears in the Geometry chapter of the ninth-grade textbook. He devoted his entire life to mathematics and made a groundbreaking contribution to Geometry.
Mathematicians of Modern Days
There is no doubt that mathematics has always been one of the most influential fields of study. With the help of the discoveries of ancient mathematicians, further studies are continuing. One of the best mathematicians today is Terence Tao, a former child prodigy who comes in the category of people with the highest I.Q. Keith Devlin and Andrew Sarnak also come to the list of top mathematicians today.
We can say that Archimedes is the Father of Mathematics. But, there is no answer to the question of who founded mathematics. It was discovered by numerous individuals throughout many millennia. We believe it is more accurate to say that the entire earth is accountable for mathematics and that humanity is responsible for its discovery.